Раскрываем Секреты Трапеции: Свойства её Диагоналей

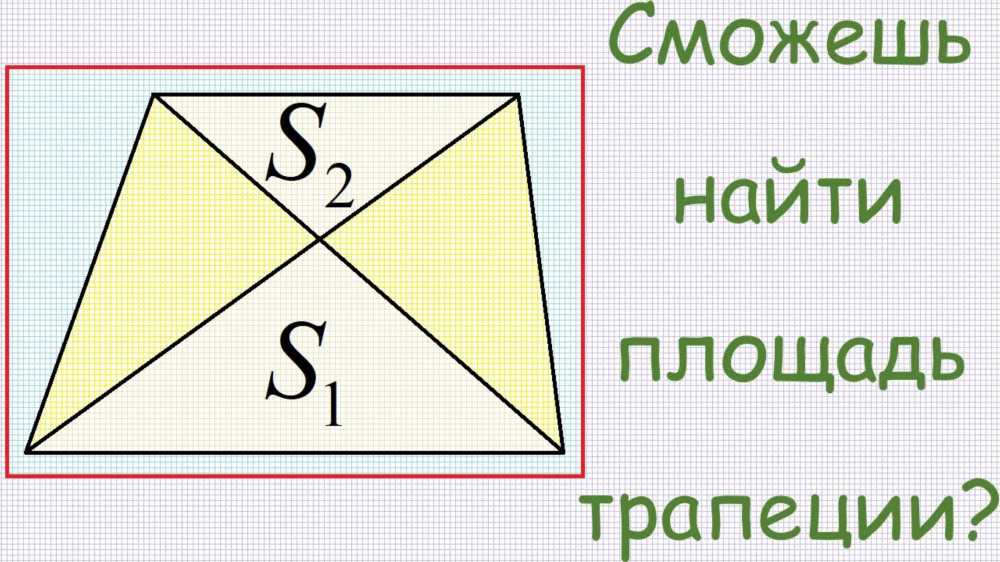
В мире геометрии трапеция занимает особое место, и её свойства могут скрывать удивительные тайны. Одним из ключевых элементов трапеции являются её диагонали, которые играют важную роль в определении формы и характеристик этой фигуры. В этой статье мы погрузимся в мир диагоналей трапеции, выявим их особенности и рассмотрим, как эти линии влияют на различные аспекты этой фигуры.

1. Определение трапеции: Быстрый обзор

Прежде чем мы погрузимся в свойства диагоналей трапеции, давайте освежим в памяти основные характеристики этой геометрической фигуры. Трапеция - это четырехугольник с двумя параллельными сторонами, из которых одна короче другой. Мы будем рассматривать различные типы трапеций, чтобы полностью охватить широкий диапазон свойств диагоналей.

2. Диагонали трапеции: Определение и основные характеристики

Диагональ трапеции - это отрезок, соединяющий два несмежных угла внутри фигуры. Давайте рассмотрим основные характеристики диагоналей трапеции:

2.1. Длина диагоналей

Длина диагоналей трапеции может различаться в зависимости от формы и размеров самой фигуры. Важно выяснить, как длины диагоналей влияют на другие параметры трапеции.

2.2. Углы между диагоналями

Исследование углов между диагоналями может привести к интересным выводам о взаимосвязи внутри трапеции. Как изменение угла влияет на соотношение длин диагоналей?

3. Свойства диагоналей трапеции

Теперь давайте перейдем к основным свойствам диагоналей трапеции, которые формируют её уникальные характеристики.

3.1. Деление трапеции на два треугольника

Диагонали трапеции разбивают фигуру на два треугольника. Как это деление влияет на площади и другие характеристики треугольников?

3.2. Секущие линии и углы

Диагонали, как секущие линии, могут создавать интересные углы внутри трапеции. Какие закономерности можно выявить в углах, образованных диагоналями?

3.3. Равенство диагоналей в определенных случаях

В некоторых типах трапеций диагонали могут оказаться равными. Как это влияет на геометрические и числовые характеристики трапеции?

4. Применение свойств диагоналей в практике

Наконец, давайте рассмотрим практическое применение этих свойств в реальных сценариях. Как можно использовать знания о диагоналях трапеции в геометрических расчетах или строительстве?

Заключение

Свойства диагоналей трапеции могут быть увлекательным объектом исследования в области геометрии. Изучение и понимание этих свойств не только раскрывает тайны фигуры, но и может привести к новым открытиям в математике и её приложениях. Погрузитесь в мир диагоналей трапеции и раскройте его потенциал!